1-1
Find a method similar to the remainder method for the integer numbers that applies to fractional numbers – as in converting: \(0.379_{10} = 0.???_2\)
1-2
Consider the two decimal numbers:
\(M = 3892.74\)
\(N = 9341.65\)
Convert them to bases \(2\) and \(16\) , and then add & subtract them in those bases.
1-A
Which is the largest binary number that can be expressed with \(15\) bits?
What are the equivalent decimal and hexadecimal numbers?
1-B
Consider a system that contains \(32K\) bytes. Assume that we are using byte addressing, that is each byte will need to have its own address, and therefore we will need \(32K\) different addresses. For convenience all addresses will have the same number \(n\) of bits, and \(n\) should be as small as possible.
What is the value of \(n\) ?
1-C
The numbers in each of the following equalities are all expressed in the same base \(r\) . Determine this radix (base) \(r\) in each case for the following operations to be correct:
a) \(14 / 2 = 5\)
b) \(54 / 4 = 13\)
1 - 12
Perform these binary multiplications:
a) \(1101 * 1011\)
b) \(0101 * 1010\)
c) \(100111 * 011011\)
1 - 14
A limited number system uses base \(12\) . There are at most four integer digits. The weights of the digits are \(12^3\), \(12^2\), \(12\), and \(1\) . Special names are given to the weights of the digits as follows: \(12 = 1\) dozen, \(12^2 =\) gross, and \(12^3 = 1\) great gross.
a) How many beverage companies are in \(6\;great\;gross\;+\;8\;gross\;+\;7\;dozen\;+\;4\) ?
b) Find the representation in base \(12\) for \(7569_{10}\) beverage cans.
1 - 16
In each of the following cases, determine the radix \(r\) :
a) \(BEE_r = 2699_{10}\)
b) \(365_r = 194_{10}\)
3 - 1
Why does the \(1\)s complement subtraction algorithm work?
3 - A
Do the following conversion problems:
a) Convert \(34.4375_{10}\) to binary.
b) Calculate the binary equivalent of \(1/3\) to \(8\) binary places, enter the result, then, after converting back to decimal consider how close it is to \(1/3\).
c) Convert the binary result of b) to hexadecimal and enter result. Then convert the hexadecimal decimal and consider: is it the same as from binary?
3 - B
Determine the base \(x\) , if \(211_x = 152_8\) .
3 - C
Noting that \(3^2 = 9\), formulate a procedure to convert from base \(3\) to base \(9\) . Use it to convert \(2110201102220112_3\) to base \(9\) .
3 - D
The solutions to the quadratic equasion \(x^2 - 11x + 22 = 0\) are \(x = 3\) and \(x = 6\) . Determine the base of the numbers in the equasion.
3 - E
Convert the hexadecimal number \(68BE\) to binary, then convert it to octal, and then to base \(32\) .

1
Solve the problem of independent switches for \(n = 4\).
Create a both the truth table and the 4D hypercube representations.
2
Write all axioms and properties for Boolean algebra sets:
\(S = set\), \(\space S \neq \varnothing\)
\((P(S),\space \bigcup,\space \bigcap,\space \complement,\space S,\space \varnothing)\)
\(P(S)\) is the set of all of subsets of \(S\); remember: if \(S\) has \(n\) elements, then \(P(S)\) has \(2^n\).
1
Prove all properties 8 – 12 using axioms 1 – 6 and the properties you just proved. Write all axioms and properties for Boolean algebra sets.
Note: for property 11, Associativity, use truth tables on the variables and assume only the values of the two-element Boolean algebra, namely \(\space B = \{0, 1\}\space\), also called “switching algebra”.


By substitution the Boolean expression equivalent of the binary operation as defined in Table of Sixteen Functions on Two Variables, show the following:
a) The Inhibition operation is neither commutative nor associative;
b) The Exclusive OR (XOR) operation is both commutative and associative.
Write Boolean expressions and construct the truth tables describing the outputs of the circuits described by these logic diagrams:
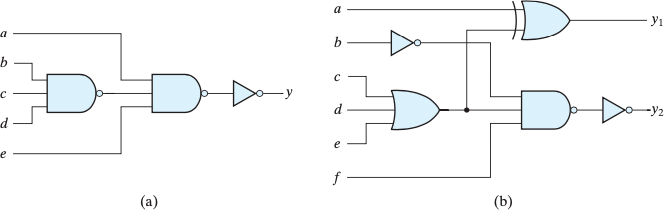




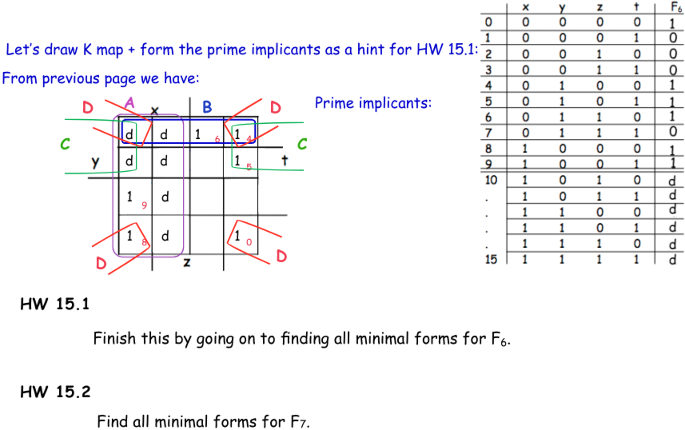


17.2 From Homework 15 - but using the Tabulation Method and the Prime Implicant Table.
17.3 Construct a Half Adder using only NOR gates. Inverters are allowed.
17.4 Construct a Full Adder using only HA’s and one other gate.
18.1 Continue the Full Adder proof from Lecture 17. Show that \(S = S_2\) and that \(C_{out} = C_1 + C_2\).
18.2 IBM Full Adder: Prove it is indeed a FA, i.e. it creates the functions \(S\) and \(C_{out}\) of a FA.
18.3 Finish and minimize functions \(D\) and \(β_{out}\) for a Full Subtractor.
18.4 Construct a Full Subtractor using only Half Subtractors and one other gate.
18.5 Express the function: \(f_> = 1\) \(\longleftrightarrow\) \(A > B\).
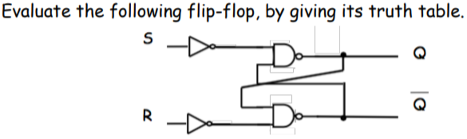
HOMEWORK 20
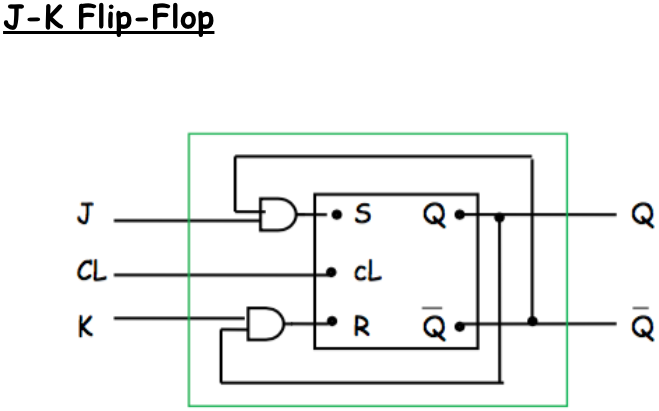
Evaluate the J-K FlipFlop. Describe its performance. For the truth table consider as inputs J and K only. Exclude the case \(J = K = 1\) from this truth table, and treat it separately.